I've been working on this problem. I think I have the answer. But is it right?
Assume:
A1: a 3D sphere with radius R
A2: the sphere is filled uniformly with N light sources per cubic unit
A3: the luminosity of each light source is L
A4: for whatever reason, the luminosity of the source falls by (1-r/R)^2
Problem:
Using:
* R = 14 billion light years
* N = 1 light source per 1 cubic giga-light year
* L = solar luminosity * 200 billion
What is the effective temperature of the sphere?
My Answer:
The first thing I did is model a single light source, at the center of the sphere. Well, I actually started with a circle, and then grew it out from there. I could then move the sphere around inside the boundary of its starting position. This would tell how many watts are leaving the boundary, and more importantly, are hitting the boundary.
I did this by filling the sphere with boxes. Nothing too fancy.
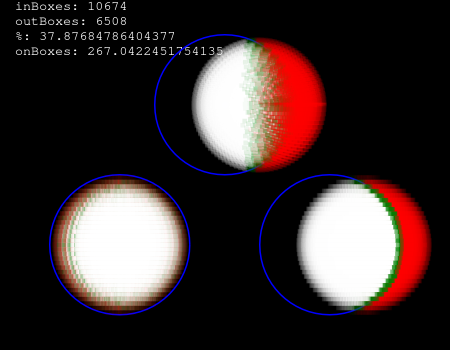
Here's the 2D version if you want see, and view source:
https://mikehelland.github.io/hubble.../cmbenergy.htm
3D version, for just a single moveable sphere:
https://mikehelland.github.io/hubble...mbenergy3d.htm
Then, create a sphere of boxes around every box in the original sphere at the origin.
https://mikehelland.github.io/hubble...nergy3dall.htm
Now I have the watts reaching the boundary, which is 0.2 megawatts. That's assuming each source is 1 watt.
If I plug the rest into this:
[tex]\displaystyle T={\sqrt[{4}]{\frac {L}{4\pi R^{2}\sigma }}}[/tex]
by doing:
That gives me 0.188.
Is that right?
Assume:
A1: a 3D sphere with radius R
A2: the sphere is filled uniformly with N light sources per cubic unit
A3: the luminosity of each light source is L
A4: for whatever reason, the luminosity of the source falls by (1-r/R)^2
Problem:
Using:
* R = 14 billion light years
* N = 1 light source per 1 cubic giga-light year
* L = solar luminosity * 200 billion
What is the effective temperature of the sphere?
My Answer:
0.188 K
The first thing I did is model a single light source, at the center of the sphere. Well, I actually started with a circle, and then grew it out from there. I could then move the sphere around inside the boundary of its starting position. This would tell how many watts are leaving the boundary, and more importantly, are hitting the boundary.
I did this by filling the sphere with boxes. Nothing too fancy.

Here's the 2D version if you want see, and view source:
https://mikehelland.github.io/hubble.../cmbenergy.htm
3D version, for just a single moveable sphere:
https://mikehelland.github.io/hubble...mbenergy3d.htm
Then, create a sphere of boxes around every box in the original sphere at the origin.
https://mikehelland.github.io/hubble...nergy3dall.htm
Now I have the watts reaching the boundary, which is 0.2 megawatts. That's assuming each source is 1 watt.
If I plug the rest into this:
[tex]\displaystyle T={\sqrt[{4}]{\frac {L}{4\pi R^{2}\sigma }}}[/tex]
by doing:
Code:
// in hundred million light years
var R = 140
// Radius in meters
const mly2mpc = 1 / 3.261564
const mpc2km = 3.08e19
var Rm = R * 100 * mly2mpc * mpc2km * 1000
var Lsol = 3.846e26
var suns = 2e11 // 200 billion suns in a galaxy
//Stefan-Boltzman constant
const sbc = 5.67e-8
T = (L * Lsol * suns / (4 * pi * sbc * Rm**2))**(1/4)
Is that right?
Aucun commentaire:
Enregistrer un commentaire